5087. Реализуйте
стек
Маша узнала о новой, модной
структуре. В ней есть “push” и “pop”.
Реализуйте стек с двумя
операциями. “Первая” операция добавляет элемент в стек, а “вторая” удаляет элемент
из стека. На каждую “вторую” операцию необходимо вывести удаленное число. Гарантируется,
что всегда есть, что удалять.
Вход. В
первой строке находится число операций n
(1 ≤ n ≤ 105).
В следующих n строках первое число –
номер операции, второе (только для “первой” операции) – добавляемое число. Это
число является натуральным и не превосходит 105.
Выход. Выведите
все удаленные числа по одному в отдельной строке.
|
Пример
входа 1 |
Пример
выхода 1 |
|
6 1 1 1 2 2 1 4 2 2 |
2 4 1 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 1 1 1 2 1 3 |
|
РЕШЕНИЕ
структуры
данных – стек
Анализ алгоритма
В задаче следует
промоделировать работу стека.
Пример
Рассмотрим
операции со стеком в первом примере:
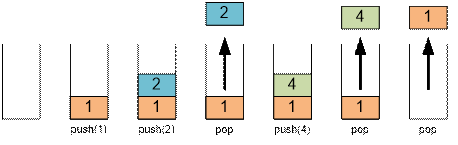
Реализация алгоритма
Объявим рабочий
стек.
stack<int> s;
Читаем количество операций n.
scanf("%d", &n);
Последовательно обрабатываем n операций.
for (int i = 0; i <
n; i++)
{
scanf("%d",
&op);
Вставка элемента, операция push.
if (op == 1)
{
scanf("%d",
&x);
s.push(x);
}
Извлечение элемента, операция pop.
else
{
printf("%d\n",
s.top());
s.pop();
}
}
Java реализация
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
Stack<Integer> s = new
Stack<Integer>();
int n = con.nextInt();
for (int i = 0;
i < n; i++)
{
int op = con.nextInt();
if (op ==
1)
{
int x = con.nextInt();
s.push(x);
}
else
System.out.println(s.pop());
}
con.close();
}
}
Java реализация –
класс MyStack
import java.util.*;
class MyStack
{
private
Vector<Integer> v;
MyStack()
{
v = new
Vector<Integer>();
}
public void
push(int x)
{
v.add(x);
}
public int
pop()
{
int last = v.lastElement();
v.remove(v.size()
- 1);
return last;
}
}
public class Main
{
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
MyStack s = new
MyStack();
int n = con.nextInt();
for (int i = 0;
i < n; i++)
{
int op = con.nextInt();
if (op ==
1)
{
int x = con.nextInt();
s.push(x);
}
else
System.out.println(s.pop());
}
con.close();
}
}
Python реализация
Читаем количество операций n.
n = int(input())
Список stack будем
использовать для моделирование стека.
stack = []
Последовательно обрабатываем n операций.
for i in range(n):
lst = list(map(int,input().split()))
Вставка элемента, операция push.
if (lst[0] == 1):
stack.append(lst[1])
Извлечение элемента, операция pop.
else:
print(stack.pop())